A simple method for procedurally generating 2D mazes as used in Chompston. The generated maps are “Pac-Man style” in that they are a series of interconnected corridors with no dead ends.

The maze is produced by placing a number of “builders” in an empty map and then carving out paths by moving them simultaneously until none remain. Essentially it’s a simulation of a multiplayer Light Cycles type of game performed by unskilled participants.

First we place a number of spawners in random locations in our world – a typical 2D array of cells which is initially the map is filled with solid cells.

At the spawner locations we place between two and four builders, each of which is assigned one of the four available directions. There needs to be at least two builders per spawner to avoid dead-ends in our maze. Each builder is also assigned a random distance it will travel before changing direction.

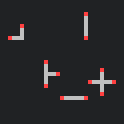
All the builders are moved simultaneously in their current direction, clearing cells in the map as they go. With every iteration each builder’s remaining travel distance is decreased.

When a builder’s remaining travel distance reaches zero it turns 90 degress left or right and we assign a new random distance to it. If they reach the edge of the world they also turn left or right.

A builder is removed when it encounters an empty cell, so we just need to continue iterating until none remain.

The finished maze, but we’ve produced a few little rooms so it’s not strictly Pac-Man-like.

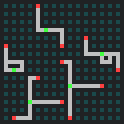
Ensuring our maze comprises single-block wide corridors is simple – constrain the placement of spawners to every other column and row of the 2D grid and always move the builders for an even number of steps before changing direction.

In this instance the maze was generated by placing five spawners and moving each builder between two and ten blocks before changing direction. By encapsulating the generation algorithm in a function that accepts a few parameters we gain some control of the flavour of the maps it produces. So with a maze generation function defined as:

BuildMap(Spawners,MinimumDistance,MaximumDistance)

the random mazes produced have characteristics similar to the following:

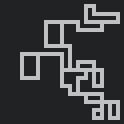
Implementing this technique for procedural maze generation in Chompston allowed me to progressively increase the complexity of the random maps through successive levels.